How To Find The Focal Length Of A Lens

Thin Lenses and Ray Tracing

Ray tracing is the technique of determining the paths light rays take; often thin lenses (the calorie-free ray bending only in one case) are causeless.

Learning Objectives

Draw backdrop of a thin lens and the purpose of ray tracing

Key Takeaways

Primal Points

• When lite interacts with objects several times every bit large equally its wavelength, it travels in straight lines and acts like a ray. A ray is simply a straight line that originates at a point.
• Ray tracing is the method for determining the paths lite takes through affair, such as optical systems that include lenses.
• A thin lens is defined every bit i with a thickness that allows rays to refract, as illustrated in, but that does not allow properties such as dispersion and aberrations. An platonic thin lens has two refracting surfaces but the lens is thin enough to assume that low-cal rays bend only in one case.
• There are five bones rules for tracing rays through a lens.

Central Terms

• focal point: A focus—a bespeak at which rays of light or other radiation converge.
• ray tracing: A technique used in optics for analysis of optical systems.
• thin lens: A sparse lens is defined to be one whose thickness allows rays to refract merely does not let properties such as dispersion and aberrations.

Thin Lenses and Ray Tracing

Ray tracing is the technique of determining or following (tracing) the paths that light rays take. Experiments, as well as our own experiences, show that when light interacts with objects several times every bit big as its wavelength, it travels in straight lines and acts like a ray. (A ray is simply a directly line that originates at a point. ) Its moving ridge characteristics are not pronounced in such situations. Since the wavelength of light is less than a micron (a thousandth of a millimeter), information technology acts similar a ray in the many common situations in which it encounters objects larger than a micron, such equally lenses.

For rays passing through thing, the constabulary of refraction is used to trace the paths. Here we use ray tracing to aid us sympathize the action of lenses in situations ranging from forming images on film to magnifying modest impress to correcting nearsightedness. While ray tracing for complicated lenses, such equally those found in sophisticated cameras, may crave computer techniques, in that location is a set of simple rules for tracing rays through thin lenses. A thin lens is divers to be one whose thickness allows rays to refract, as illustrated in, but does not allow properties such as dispersion and aberrations. An ideal thin lens has two refracting surfaces only the lens is thin enough toassume that lite rays bend simply once. Some other mode of saying this is that the lens thickness is much much smaller than the focal length of the lens. A thin symmetrical lens has two focal points, one on either side and both at the same distance from the lens. (Run into. ) Another important characteristic of a thin lens is that lite rays through its center are deflected by a negligible amount, as seen in the center rays in the first two figures. The treatment of a lens equally a thin lens is known equally the "sparse lens approximation. "

Convex Lens: Rays of lite entering a converging lens parallel to its centrality converge at its focal point F. (Ray 2 lies on the axis of the lens. ) The distance from the center of the lens to the focal point is the lens'southward focal length f. An expanded view of the path taken by ray 1 shows the perpendiculars and the angles of incidence and refraction at both surfaces.

Thin Lens: Thin lenses have the same focal length on either side. (a) Parallel light rays entering a converging lens from the right cross at its focal signal on the left. (b) Parallel light rays inbound a diverging lens from the right seem to come up from the focal point on the right.

Rules for Ray Tracing

Using newspaper, pencil, and a direct edge, ray tracing can accurately describe the performance of a lens. The rules for ray tracing for thin lenses are based on the illustrations included in this section:

1. A ray entering a converging lens parallel to its axis passes through the focal point F of the lens on the other side. ( Run into rays ane and 3 in. )
2. A ray entering a diverging lens parallel to its axis seems to come from the focal signal F. (See rays ane and 3 in. )
3. A ray passing through the center of either a converging or a diverging lens does not change direction. (See ray two in and. )
4. A ray entering a converging lens through its focal point exits parallel to its axis. (The reverse of rays 1 and 3 in. )
5. A ray that enters a diverging lens past heading toward the focal point on the opposite side exits parallel to the axis. (The reverse of rays 1 and 3 in ).

Diverging Lens: Rays of light entering a diverging lens parallel to its axis are diverged, and all appear to originate at its focal signal F. The dashed lines are not rays—they signal the directions from which the rays appear to come. The focal length f of a diverging lens is negative. An expanded view of the path taken by ray 1 shows the perpendiculars and the angles of incidence and refraction at both surfaces.

Ray Diagrams, Concave Lens and Convex Mirror: Shows how to describe the ray diagrams for locating the prototype produced by a concave lens and a convex mirror.

The Thin Lens Equation and Magnification

The thin lens equation relates the object distance d_o , prototype distance d_i , and focal length f.

Learning Objectives

Formulate five basic rules of ray tracing

Key Takeaways

Key Points

• Ray tracing can be used to construct an image from the light rays originating from an object that pass through a lens. The image is located at the point where the rays cross. Past choosing several points from an object the entire paradigm tin be constructed.
• We define practice to be the object distance, the distance of an object from the middle of a lens. Image distance di is divers to be the distance of the image from the center of a lens. The height of the object and superlative of the image are given the symbols ho and how-do-you-do, respectively.
• The thin lens equation rapidly provides the relation between d_i , d_o , and the focal length f. Information technology tin can exist derived from a geometric analysis of ray tracing for thin lenses and is given by [latex]\frac{ane}{\text{d}_\text{o}}+\frac{1}{\text{d}_\text{i}}=\frac{1}{\text{f}}[/latex].
• The magnification m of an image is the ratio between the image and object meridian (h_i /h_o ). The magnification is related to d_o , d_i , h_o , and h_i by the following relation: [latex]\frac{\text{h}_\text{i}}{\text{h}_\text{o}}=-\frac{\text{d}_\text{i}}{\text{d}_\text{o}}=\text{thousand}[/latex].

Cardinal Terms

• thin lens equation: Relates object altitude practise, paradigm altitude di, and focal length f: [latex]\frac{1}{\text{d}_\text{o}}+\frac{one}{\text{d}_\text{i}}=\frac{1}{\text{f}}[/latex]
• paradigm distance: The distance of the image from the center of the lens.
• magnification: The credible enlargement of an object in an image.

The Thin Lens Equation and Magnification

Prototype Formation by Sparse Lenses

How does a lens form an prototype of an object? We can use the technique of ray tracing to illustrate how lenses form images. We tin can also develop equations to describe the images quantitatively. Remember the five basic rules of ray tracing:

1. A ray inbound a converging lens parallel to its axis passes through the focal point F of the lens on the other side.
2. A ray inbound a diverging lens parallel to its axis seems to come up from the focal indicate F.
3. A ray passing through the center of either a converging or a diverging lens does not alter direction.
4. A ray inbound a converging lens through its focal indicate exits parallel to its axis.
5. A ray that enters a diverging lens by heading toward the focal signal on the contrary side exits parallel to the axis.

Consider an object some altitude away from a converging lens, as shown in. To find the location and size of the image formed, we trace the paths of selected light rays originating from one point on the object (in this instance the meridian of the person's head). The figure shows iii rays from the top of the object that can be traced using the five ray tracing rules. Rays get out this point going in many directions, but we concentrate on only a few with paths that are piece of cake to trace. The first ray is one that enters the lens parallel to its axis and passes through the focal point on the other side (rule 1). The second ray passes through the center of the lens without changing direction (rule three). The tertiary ray passes through the nearer focal betoken on its way into the lens and leaves the lens parallel to its axis (rule 4). The three rays cross at the same betoken on the other side of the lens. The image of the top of the person's head is located at this signal. All rays that come up from the same point on the top of the person'southward head are refracted in such a mode every bit to cantankerous at the point shown. Rays from some other bespeak on the object, such as her chugalug buckle, will also cross at another common point, forming a consummate image, as shown. Although three rays are traced in, only 2 are necessary to locate the image. It is best to trace rays for which there are unproblematic ray tracing rules. Before applying ray tracing to other situations, permit us consider the example shown in in more detail.

Image Formation with a Thin Lens: Ray tracing is used to locate the epitome formed by a lens. Rays originating from the same point on the object are traced—the 3 chosen rays each follow one of the rules for ray tracing, so that their paths are easy to decide. The image is located at the point where the rays cantankerous. In this case, a real image—one that can be projected on a screen—is formed.

Several important distances appear in. Nosotros define d_o as the object altitude—the distance of an object from the center of a lens. Image distance d_i is defined as the altitude of the image from the eye of a lens. The height of the object and height of the image are given the symbols h_o and h_i , respectively. Images that appear upright relative to the object have heights that are positive and those that are inverted accept negative heights. Using the rules of ray tracing and making a scale drawing with newspaper and pencil, similar that in, nosotros can accurately depict the location and size of an epitome. But the real benefit of ray tracing is in visualizing how images are formed in a variety of situations. To obtain numerical information, we employ a pair of equations that can exist derived from a geometric analysis of ray tracing for thin lenses. The thin lens equation is:

[latex]\frac{ane}{\text{d}_\text{o}}+\frac{i}{\text{d}_\text{i}}=\frac{one}{\text{f}}[/latex]

Nosotros define the ratio of image height to object height (h_i /h_o ) every bit the magnification m. The magnification is related to d_o , d_i , h_o , and h_i by the post-obit relation:

[latex]\frac{\text{h}_\text{i}}{\text{h}_\text{o}}=-\frac{\text{d}_\text{i}}{\text{d}_\text{o}}=\text{m}[/latex]

In many cases both of these equations are referred to together as the thin lens equations. The sparse lens equations are broadly applicative to all situations involving sparse lenses (and "sparse" mirrors).

Sparse Lens Equations for a Convex Lens: Shows how to use the sparse lens equation to calculate the paradigm distance, image height and image orientation for convex lenses when the object distance is greater the the focal length (f).

Combinations of Lenses

A compound lens is an array of uncomplicated lenses with a common centrality.

Learning Objectives

Summate focal length for a compound lens from the focal lengths of uncomplicated lenses

Key Takeaways

Central Points

• The use of multiple elements allows for the correction of more optical aberrations, such as the chromatic abberation caused by the wavelength -dependent index of refraction in drinking glass, than is possible using a single lens.
• If the lenses of focal lengths f_i and f₂ are "thin", the combined focal length f of the lenses is given by [latex]\frac{1}{\text{f}}=\frac{1}{\text{f}_1}+\frac{ane}{\text{f}_2}[/latex]while if the lenses are separated by some distance d then the combined focal length is given by [latex]\frac{ane}{\text{f}}=\frac{one}{\text{f}_1}+\frac{1}{\text{f}_2}-\frac{\text{d}}{\text{f}_1 \text{f}_2}[/latex].
• If the separation altitude is equal to the sum of the focal lengths (d = f_i +f₂ ), the combined focal length is space. This corresponds to a pair of lenses that transform a collimated beam into some other collimated axle. This type of system is called an afocal system (a uncomplicated optical telescope).
• An achromatic doublet is a kind of compound lens designed to bring two wavelengths (typically red and blue/violet) into focus in the same plane. This (partially) corrects for the chromatic aberration constitute in a unmarried simple lens. Encounter.

Cardinal Terms

• abnormality: The convergence to different foci, by a lens or mirror, of rays of low-cal emanating from one and the same point, or the deviation of such rays from a single focus; a defect in a focusing mechanism that prevents the intended focal point.
• afocal system: An optical system that produces no net convergence or divergence of the beam, i.eastward. has an infinite effective focal length. This type of system can be created with a pair of optical elements where the distance between the elements is equal to the sum of each chemical element'south focal length (d = f1+f2).
• achromatic doublet: A type of lens made up of 2 simple lenses paired together designed and so that the chromatic aberration of each lens partially offsets the other; in this way light in a range of wavelengths may be brought to the aforementioned focus.

COMPOUND LENSES

In contrast to a unproblematic lens, which consists of just ane optical chemical element, a chemical compound lens is an array of elementary lenses (elements) with a common axis. The use of multiple elements allows for the correction of more optical aberrations, such as the chromatic abnormality caused by the wavelength-dependent index of refraction in glass, than is possible using a unmarried lens. In many cases these aberrations can exist compensated for to a cracking extent by using a combination of uncomplicated lenses with complementary aberrations.

The simplest example is where lenses are placed in contact: if the lenses of focal lengths f ₁ and f ₂ are "thin", the combined focal length f of the lenses is given by

[latex]\frac{1}{\text{f}}=\frac{i}{\text{f}_1}+\frac{1}{\text{f}_2}[/latex].

Since 1/f is the ability of a lens, information technology can be seen that the powers of thin lenses in contact are additive.

If two sparse lenses are separated in air by some distance d (where d is smaller than the focal length of the first lens), the focal length for the combined organisation is given by

[latex]\frac{1}{\text{f}}=\frac{1}{\text{f}_1}+\frac{i}{\text{f}_2}-\frac{\text{d}}{\text{f}_1 \text{f}_2}[/latex].

BACK FOCAL LENGTH

The altitude from the second lens to the focal point of the combined lenses is called the back focal length (BFL).

[latex]\text{BFL}=\frac{\text{f}_2(\text{d}-\text{f}_1)}{\text{d}-(\text{f}_1+\text{f}_2)}[/latex].

Every bit d tends to nil, the value of the BFL tends to the value of f given for sparse lenses in contact.

If the separation distance is equal to the sum of the focal lengths (d = f ₁+f ₂), the combined focal length and BFL are space. This corresponds to a pair of lenses that transform a parallel (collimated) beam into another collimated beam (see ). This type of arrangement is called an afocal arrangement, since information technology produces no net convergence or difference of the beam. Two lenses at this separation form the simplest type of optical telescope. Although the system does non modify the divergence of a collimated beam, information technology does change the width of the beam. The magnification of such a telescope is given past

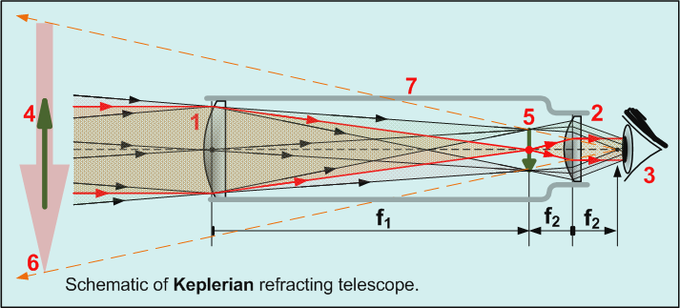
Keplerian Telescope: All refracting telescopes employ the same principles. The combination of an objective lens 1 and some type of eyepiece 2 is used to get together more than light than the human eye could collect on its ain, focus it 5, and present the viewer with a brighter, clearer, and magnified virtual epitome 6. The magnification tin can be establish by dividing the focal length of the objective lens past the focal length of the eyepiece.

[latex]\text{One thousand}=-\frac{\text{f}_2}{\text{f}_1}[/latex]

which is the ratio of the input beam width to the output axle width. Note the sign convention: a telescope with ii convex lenses (f ₁ > 0, f ₂ > 0) produces a negative magnification, indicating an inverted image. A convex plus a concave lens (f _ane > 0 >f ₂) produces a positive magnification and the epitome is upright.

ACHROMATS

An achromatic lens or achromat is a lens that is designed to limit the effects of chromatic and spherical aberration. Achromatic lenses are corrected to bring ii wavelengths (typically red and blue/violet) into focus in the aforementioned aeroplane.

The most mutual blazon of achromat is the achromatic doublet, which is composed of two individual lenses made from spectacles with different amounts of dispersion Typically, one element is a negative (concave) element made out of flint, which has relatively high dispersion, and the other is a positive (convex) chemical element made of crown glass, which has lower dispersion. The lens elements are mounted next to each other, often cemented together, and shaped so that the chromatic aberration of one is counterbalanced by that of the other.

In the near common type (shown in ), the positive power of the crown lens chemical element is non quite equaled by the negative ability of the flintstone lens element. Together they grade a weak positive lens that will bring 2 unlike wavelengths of light to a common focus. Negative doublets, in which the negative-power element predominates, are too made.

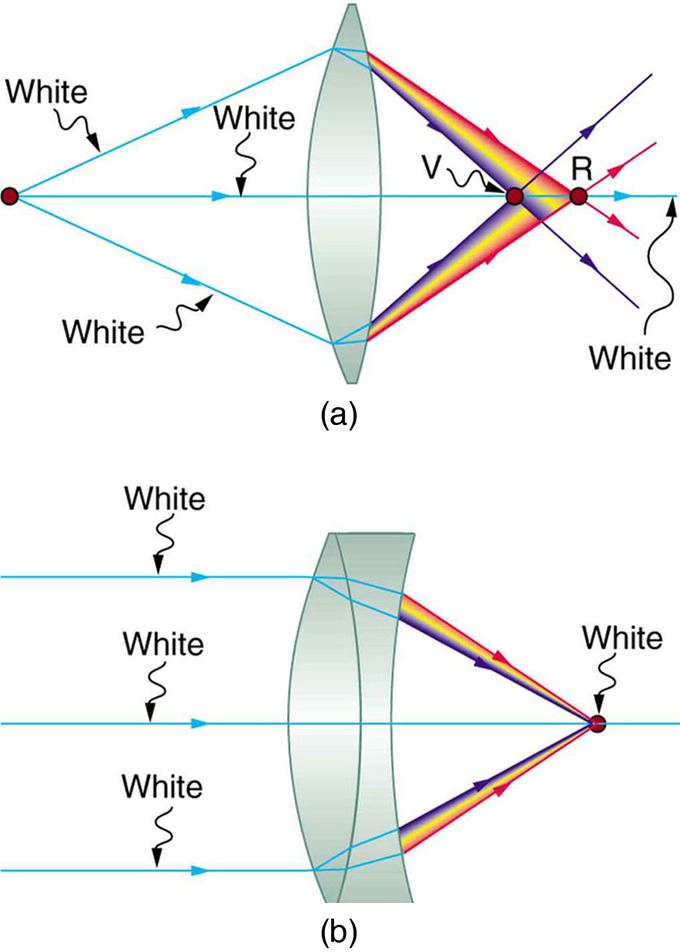
Achromatic Doublet: (a) Chromatic aberration is acquired by the dependence of a lens's alphabetize of refraction on color (wavelength). The lens is more powerful for violet (V) than for red (R), producing images with dissimilar locations and magnifications. (b) Multiple-lens systems, such equally this achromatic doublet, can partially right chromatic aberrations, but they may require lenses of unlike materials and add to the expense of optical systems such as cameras.

The Lensmaker's Equation

The lensmaker's formula is used to relate the radii of curvature, the thickness, the refractive index, and the focal length of a thick lens.

Learning Objectives

Compare idealized thin lenses with real lenses

Central Takeaways

Primal Points

• If a lens is biconvex, a axle of lite travelling parallel to the lens centrality and passing through the lens will be focused to a spot on the axis, at a certain distance behind the lens (i.east. the focal length ). In this case, the lens is chosen a positive or converging lens. Come across.
• If a lens is biconcave, a axle of calorie-free passing through the lens is diverged (spread); the lens is thus called a negative or diverging lens. See.
• The focal length of a thick lens in air tin can be calculated from the lensmaker's equation: [latex]\text{P}=\frac{1}{\text{f}}=(\text{n}-1)[\frac{1}{\text{R}_1}-\frac{one}{\text{R}_2}+\frac{(\text{n}-1)\text{d}}{\text{northward} \text{R}_1 \text{R}_2}][/latex].
• The signs of the lens' radii of curvature indicate whether the corresponding surfaces are convex or concave. The signs are reversed for the back surface of the lens: if R₂ is positive the surface is concave, and if R₂ is negative the surface is convex.
• The lensmaker'south equation tin can be profoundly simplified if the lens thickness d is very pocket-size compared to R₁ and R₂ . In this case, the thin lens approximation can then exist made and the lensmaker's equation can be approximated every bit [latex]\text{P}=\frac{1}{\text{f}} \approx (\text{n}-ane)[\frac{one}{\text{R}_1}-\frac{1}{\text{R}_2}][/latex].

Key Terms

• thick lens: Lenses whose thicknesses are non negligible (i.e., one cannot make the simple assumption that a light ray is refracted only once in the lens).
• surface vertices: The points where each surface crosses the optical axis. They are of import primarily because they are the physically measurable parameters for the position of the optical elements, and and then the positions of the other primal points must exist known with respect to the vertices to describe the physical system.

The Lensmaker's Equation

Thick Lenses

Unlike idealized thin lenses, real lenses have a finite thickness between their two surfaces of curvature. An ideal thin lens with 2 surfaces of equal curvature would have zero optical power, meaning that information technology would neither converge nor diverge lite. A lens whose thickness is not negligible is called a thick lens. In this case, we can not but assume that a low-cal ray is only refracted once while traveling through the lens. Instead the extent of the refraction must be dependent on the thickness of the lens.

Lenses are classified by the curvature of the 2 optical surfaces. A lens is arched (or double convex, or just convex) if both surfaces are convex. If the lens is biconvex, a axle of light travelling parallel to the lens centrality and passing through the lens volition be converged (or focused) to a spot on the axis, at a certain distance behind the lens (i.e. the focal length). In this case, the lens is called a positive or converging lens. See for a diagram of a positive (converging) lens.

Thick Converging Lens: Diagram of a positive (converging) lens. The lensmaker'southward formula relates the radii of curvature, the index of refraction of the lens, the thickness of the lens, and the focal length.

If the lens is biconcave, a beam of lite passing through the lens is diverged (spread); the lens is thus called a negative or diverging lens. The axle after passing through the lens appears to exist emanating from a item point on the axis in forepart of the lens; the altitude from this bespeak to the lens is also known every bit the focal length, although it is negative with respect to the focal length of a converging lens. See for a diagram of a negative (diverging) lens.

Negative Diverging Lens: Diagram of a negative (diverging) lens. The lensmaker's formula relates the radii of curvature, the index of refraction of the lens, the thickness of the lens, and the focal length.

The focal length of a thick lens in air can be calculated from the lensmaker'due south equation:

[latex]\text{P}=\frac{1}{\text{f}}=(\text{n}-1)[\frac{ane}{\text{R}_1}-\frac{1}{\text{R}_2}+\frac{(\text{n}-1)\text{d}}{\text{north} \text{R}_1 \text{R}_2}][/latex]

where

• P is the ability of the lens,
• f is the focal length of the lens,
• north is the refractive index of the lens material,
• R₁ is the radius of curvature of the lens surface closest to the calorie-free source,
• R₂ is the radius of curvature of the lens surface farthest from the light source, d and is the thickness of the lens (the distance forth the lens centrality betwixt the two surface vertices).

Sign convention of Radii R₁ and R₂

The signs of the lens' radii of curvature indicate whether the corresponding surfaces are convex or concave. The sign convention used to stand for this varies, simply for our treatment if R ₁ is positive the first surface is convex, and if R _one is negative the surface is concave. The signs are reversed for the back surface of the lens: if R ₂ is positive the surface is concave, and if R _ii is negative the surface is convex. If either radius is space, the corresponding surface is apartment. With this convention the signs are determined by the shapes of the lens surfaces, and are independent of the direction in which light travels through the lens.

Sparse Lens Approximation

The above equation can exist profoundly simplified if the lens thickness d is very minor compared to R_i and R₂. In this case, the sparse lens approximation can and then be fabricated and the lensmaker'south equation can be approximated equally

[latex]\text{P}=\frac{1}{\text{f}} \approx (\text{n}-ane)[\frac{1}{\text{R}_1}-\frac{ane}{\text{R}_2}][/latex]

The focal length f is positive for converging lenses, and negative for diverging lenses. The reciprocal of the focal length, 1/f, is the optical of the lens. If the focal length is in meters, this gives the optical power in diopters (inverse meters).

Lenses have the same focal length when light travels from the dorsum to the front equally when light goes from the front end to the dorsum, although other properties of the lens, such as the aberrations are non necessarily the same in both directions.

Refraction Through Lenses

Because the index of refraction of a lens is greater than air, a ray moves towards the perpendicular every bit information technology enters and away as it leaves.

Learning Objectives

Compare the effect of a convex lens and a concave lens on the lite rays

Key Takeaways

Fundamental Points

• Recall that the a ray volition bend as it enters a medium with a unlike refractive index. Since the refractive index of a lens is greater than air, a lite ray will motility towards the perpendicular equally it enters and away as it leaves.
• A convex lens has been shaped so that all light rays that enter it parallel to its axis cross one another at a single point on the contrary side of the lens (the focal betoken ). Such a lens is called a converging (or convex) lens for the converging effect it has on low-cal rays. See.
• A concave lens is a diverging lens, because it causes the lite rays to bend away (diverge) from its axis. shows the result it has on rays of lite that enter it parallel to its axis (the path taken past ray two in the figure is the axis of the lens).
• The greater issue a lens has on low-cal rays, the more powerful information technology is said to exist. A powerful converging lens will focus parallel low-cal rays closer to itself and will have a smaller focal length than a weak lens. The ability of a lens is given by the equation [latex]\text{P}=\frac{1}{\text{f}}[/latex].

Key Terms

• convex lens: A lens having at least 1 convex surface, such that light passing through it, may be brought to a focus.
• concave lens: A lens having at least i concave surface, such that light rays passing through it bend away from its optical axis.
• focal point: A focus—a point at which rays of low-cal or other radiation converge.

Refraction Through Lenses

Lenses are found in a huge assortment of optical instruments, ranging from the elementary magnifying glass to a camera lens to the lens of the human center. The discussion lens derives from the Latin word for lentil edible bean—the shape of which is similar to that of the convex lens (every bit shown in ). The convex lens is shaped so that all light rays that enter it parallel to its axis cantankerous one another at a single indicate on the opposite side of the lens. The axis is defined every bit a line normal to the lens at its center (as shown in ). Such a lens is chosen a converging (or convex) lens for the corresponding issue it has on light rays. The expanded view of the path of one ray through the lens illustrates how the ray changes direction both every bit it enters and as it leaves the lens.

Since the index of refraction of the lens is greater than that of air, the ray moves towards the perpendicular as it enters, and abroad from the perpendicular as it leaves (this is in accordance with the police of refraction). Due to the lens'due south shape, light is thus bent toward the axis at both surfaces. The point at which the rays cross is divers as the focal point F of the lens. The distance from the eye of the lens to its focal point is defined as the focal length f of the lens. shows how a converging lens, such as that in a magnifying drinking glass, can concentrate (converge) the well-nigh parallel light rays from the dominicus towards a small spot.

Magnifying Drinking glass: Sunlight focused by a converging magnifying glass tin burn paper. Light rays from the sun are nearly parallel and cantankerous at the focal point of the lens. The more than powerful the lens, the closer to the lens the rays volition cross.

The greater issue a lens has on low-cal rays, the more than powerful information technology is said to be. For example, a powerful converging lens will focus parallel light rays closer to itself and will have a smaller focal length than a weak lens. The light will likewise focus into a smaller, more than intense spot for a more powerful lens. The power P of a lens is divers as the inverse of its focal length. In equation class:

[latex]\text{P}=\frac{ane}{\text{f}}[/latex]

shows the effect of a concave lens on rays of light entering it parallel to its axis (the path taken by ray 2 in the effigy is the axis of the lens). The concave lens is a diverging lens, considering it causes the light rays to curve away (diverge) from its axis. In this case, the lens is shaped so that all low-cal rays entering it parallel to its axis appear to originate from the same indicate F, defined as the focal betoken of a diverging lens. The distance from the center of the lens to the focal betoken is once more called the focal length f of the lens. Note that the focal length and power of a diverging lens are divers as negative. For case, if the distance to F in is v.00 cm, and so the focal length is f=–5.00 cm and the power of the lens is P=–20 D. The expanded view of the path of one ray through the lens illustrates how the shape of the lens (given the constabulary of refraction) causes the ray to follow its particular path and be diverged.

In subsequent sections we volition examine the technique of ray tracing to draw the formation of images by lenses. Additionally, we will explore how image locations and characteristics can be quantified with the help of a prepare of geometric eyes equations.

Source: https://courses.lumenlearning.com/boundless-physics/chapter/lenses/

Posted by: prevostnotheires.blogspot.com

Share this post